Три перпендикулярные плоскости. Проецирование на три взаимно перпендикулярные плоскости проекции

Существует множество деталей, информацию о форме которых невозможно передать двумя проекциями чертежа. Для того чтобы информация о сложной форме детали была представлена достаточно полно, используют проецирование на три взаимно перпендикулярные плоскости проекции: фронтальную - V, горизонтальную - Н и профильную - W (читается «дубль вэ»).

Комплексным чертежом Чертеж представленный тремя видами или проекциями, в большинстве случаев дает полное представление о форме и конструкции детали (предмета и объекта) и также называется комплексным чертежом. осным чертежом. Если чертеж построен с осями координат, он называется осным чертежом. безосным Если чертеж построен без осей координат, он называется безосным профильной Если плоскость W перпендикулярна к фронтальной и горизонтальной плоскостям проекций, то она называется профильной

В трехгранный угол помещают предмет так, чтобы его формообразующая грань и основание были бы параллельны соответственно фронтальной и горизонтальной плоскостям проекций. Затем через все точки предмета проводят проецирующие лучи, перпендикулярные всем трем плоскостям проекций, на которых получают фронтальную, горизонтальную и профильную проекции предмета. После проецирования предмет удаляют из трехгранного угла, а затем горизонтальную и профильную плоскости проекций поворачивают на 90° соответственно вокруг осей Ох иOz до совмещения с фронтальной плоскостью проекции и получают чертеж детали, содержащий три проекции.

Три проекции чертежа взаимосвязаны друг с другом. Фронтальная и горизонтальная проекции сохраняют проекционную связь изображений, т. е. устанавливаются проекционные связи и между фронтальной и горизонтальной, фронтальной и профильной, а также горизонтальной и профильной проекциями. Линии проекционной связи определяют местоположение каждой проекции на поле чертежа. Форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела в системе трех проекций на производстве

1.Грани параллельные плоскости проекций проецируются на нее без искажения, в натуральную величину. 2.Грани перпендикулярные к плоскости проекций, проецируются в отрезке прямых линий. 3.Грани расположенные наклонно к плоскостям проекций, изображения на ней с искажением (уменьшенными)

& 3. стр вопросы письменно задание 4.1. стр стр, & 5, стр.37-45, вопросы письменно задание

Обратимость чертежа, т. е. однозначное определение положения точки в пространстве по ее проекциям, может быть обеспечена проецированием на две непараллельные плоскости проекций.

Для удобства проецирования в качестве двух плоскостей проекций выбирают две взаимно перпендикулярные плоскости (рис. 1.11). Одну из них принято располагать горизонтально – ее называют горизонтальной плоскостью проекций , другую – вертикально, параллельно плоскости чертежа. Такую вертикальную плоскость называют фронтальной плоскостью проекций . Эти плоскости проекций пересекаются по линии, называемой осью проекций .

Ось проекций разделяет каждую из плоскостей проекций на две полуплоскости, или полы.

Обозначим плоскости проекций: π2 – фронтальную, π, – горизонтальную, ось проекций – буквой x или в виде дроби π2/ π1 . Плоскости проекций π2 и π, образуют систему π2, π,.

Плоскости проекций, пересекаясь, образуют четыре двугранных угла, из которых приведенный на рис. 1.11 (с обозначениями граней π2, π1) считают первым.

В промышленности чертежи многих деталей выполняют также в системе двух взаимно перпендикулярных плоскостей, пересекающихся по вертикальной оси проекций ζ (рис. 1.12). При этом фронтальной плоскостью проекций оставляют также плоскость π2, а перпендикулярную ей и обозначаемую π3, называют .

В системе двух взаимно перпендикулярных плоскостей проекций: горизонтальной проекцией точки называют прямоугольную проекцию точки на горизонтальной плоскости проекций;

фронтальной проекцией точки называют прямоугольную проекцию точки на фронтальной плоскости проекций.

Наглядное изображение построения проекций произвольной точки А в системе π2, π, показано на рис. 1.13. Горизонтальную проекцию, обозначенную А ", находят как пересечение перпендикуляра, проведенного из точки А к плоскости π, с этой плоскостью. Фронтальную проекцию, обозначенную А ", находят как пересечение перпендикуляра, проведенного из точки А к плоскости π2, с этой плоскостью.

Проецирующие прямые ΑΑ " и ΑΑ перпендикулярные к плоскостям π2 и π, принадлежат плоскости α. Она перпендикулярна плоскостям проекций и пересекает ось проекций в точке Α χ. Три взаимно перпендикулярные плоскости α, π2 и π, пересекаются по взаимно перпендикулярным прямым, τ. е. прямые А "Α χ, А Ά χ и ось χ взаимно перпендикулярны.

Построение некоторой точки А в пространстве по двум заданным ее проекциям – фронтальной А " и горизонтальной А " – показано на рис. 1.14. Точку А находят в пересечении перпендикуляров, прове-

денных из проекции А” к плоскости π2 и из проекции А " к плоскости π,. Проведенные перпендикуляры принадлежат одной плоскости α, перпендикулярной плоскостям π2 и π, и пересекаются в единственной искомой точке А пространства.

Таким образом, две прямоугольные проекции точки вполне определяют ее положение в пространстве относительно данной системы взаимно перпендикулярных плоскостей проекций.

Рассмотренное наглядное изображение точки в системе π2, π, для целей черчения неудобно ввиду сложности. Преобразуем его так, чтобы горизонтальная плоскость проекций совпала с фронтальной плоскостью проекций, образуя одну плоскость чертежа. Это преобразование осуществляют (рис. 1.15) путем поворота вокруг оси χ плоскости π, на угол 90° вниз. При этом отрезки Α χ А " и Α χ А " образуют один отрезок А "А расположенный на одном перпендикуляре к оси проекции – на линии связи. В результате указанного совмещения плоскостей π2 и πι получается чертеж – рис. 1.16, известный под названием эпюр или эпюр Монжа . Это чертеж в системе π2, π, (или в системе двух прямоугольных проекций). Без обозначения плоскостей π2 и π, этот чертеж приведен на рис. 1.17.

Гаспар Монж (1746–1818) – французский ученый, общественный и государственный деятель в период французской революции 1789–1794 гг. и правления Наполеона 1 . Накапливавшиеся с древних времен сведения и приемы изображения пространственных форм на плоскости были приведены в систему и развиты в труде Г. Монжа, изданном в 1799 г. под названием Geometric descriptive (русский перевод (13)).

Начертательную геометрию в России начали преподаватьс 1810 г. Первые труды по ней опубликованы К.И. Потье (1816) и Я.А. Севастьяновым (1821). Большой вклад в развитие начертательной геометрии внесли многие русские и советские ученые (более подробные сведения приведены в книгах , , и др.).

Проецирование на три взаимно перпендикулярные плоскости проекций

В зависимости от сложности для полного выявления наружных и внутренних форм деталей и их соединений и для решения ряда задач бывают необходимы три и более изображений. Поэтому вводят три и более плоскостей проекций.

Введем в систему π2, π, третью вертикальную плоскость проекций (рис. 1.18), перпендикулярную оси χ и соответственно фронтальной и горизонтальной плокостям проекций. Ее называют профильной плоскостью проекций и обозначают π2 (см. также рис. 1.12). Такую систему плоскостей проекций называют системой π2, π, π3. В этой системе оси проекций ζ и у являются линиями пересечения профильной плоскости проекций с фронтальной и горизонтальной. Точка О – пересечение всех трех осей проекций.

Схема совмещения трех взаимно перпендикулярных плоскостей проекций в одну плоскость чертежа показана на рис. 1.19. При этом ось у занимает два положения.

Наглядное изображение некоторой точки А, ее проекций А ", А А в системе π2, щ, π }, а также их координат приведены на рис. 1.20, ее чертеж – на рис. 1.21.

Профильной проекцией точки называется прямоугольная проекция точки на профильной плоскости проекций (например, проекция А"" на рис. 1.21).

Фронтальная и профильная проекции точки (А" и А "") лежат на одной линии связи (А " А перпендикулярной оси ζ-

Профильную проекцию точки строят несколькими способами (рис. 1.21).

Через фронтальную проекцию проводят линию связи, перпендикулярную оси ζ, и от оси г отмечают координату у а (отрезок/1 Ά χ).

Это построение можно выполнить также с помощью дуги окружности, проведенной из центра О, или с помощью прямой, проведенной под углом 45° к оси у. Первый из указанных способов предпочтителен, как более точный.

Наряду с указанными обозначениями плоскостей проекций в литературе применяют и другие обозначения, например буквами V, Η, W.
Бриге (франц.) – чертеж, проект.

При решении задач бывает недостаточно двух проекций. Поэтому вводят третью плоскость перпендикулярно плоскостям П 1 и П 2 . Ее называют профильной плоскостью (П 3 ) .

Три плоскости делят пространство на 8 частей – октантов (рис. 6). Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Чтобы получить эпюр (рис. 7) любого геометрического образа плоскости П 1 и П 3 вращают, как показано на рис. 6.

Плоскости проекций, попарно пересекаясь, определяют три оси x , y и z , которые можно рассматривать как систему декартовых координат в пространстве с началом в точке О .

Для получения эпюра точки в системе трех плоскостей проекций плоскости П 1 и П 3 вращают до совмещения с плоскостью П 2 (рис. 8). При обозначении осей на эпюре отрицательные полуоси обычно не указывают.

Для нахождения профильной проекции точки поступают следующим образом: из фронтальной проекции А 2 точки А проводят прямую перпендикулярно оси Z и на этой прямой от оси z откладывают отрезок, равный координате у точки А (рис. 9).

Рис.8 Рис. 9
Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата):

а
?
бсцисса х = ………..= …..…..= ….….. = ……….. – расстояние от точки до плоскости П 3;

ордината у = ……….= ………= …...... = ………… – расстояние от точки до плоскости П 2;

аппликата z= …….. = ………= ……..= ………… – расстояние от точки до плоскости П 1
А 1 А 2 – вертикальная линия связи, перпендикулярная оси х;

А 2 А 3 – горизонтальная линия связи, перпендикулярная оси z .
А
?
1 (….,….) Положение проекции каждой точки

А 2 (….,….) определяется двумя координатами

А 3 (….,….)
Если точка принадлежит хотя бы одной плоскости проекций, она занимает частное положение относительно плоскостей проекций. Если точка не принадлежит ни одной из плоскостей проекций, она занимает общее положение.

Лекция № 2
ПРЯМАЯ

1. Прямая. 2. Положение прямой относительно плоскостей проекций. 3. Принадлежность точки прямой. 4. Следы прямой. 5. Деление отрезка прямой в данном соотношении. 6. Определение длины отрезка прямой и углов наклона прямой к плоскостям проекций. 7. Взаимное положение прямых.
1 ПРЯМАЯ
Проекцией прямой в общем случае является прямая, за исключением случая, когда прямая перпендикулярна плоскости (рис. 10).

Чтобы построить эпюр прямой определяют координаты x , y , z двух точек прямой и переносят эти величины на чертеж.

2 ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИИ
В

зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

Проекция прямой общего положения меньше самой прямой.

Различают восходящую прямую – это прямая, которая по мере удаления от наблюдателя повышается (рис. 11) и нисходящую, которая понижается.

h   П 1 ; Z = const

h 2  0x признак

h 3  0у горизонтали

h 1 = h  – свойство

горизонтали

 – угол наклона прямой к

плоскости П 1

 – угол наклона прямой к

плоскости П 2

 – угол наклона прямой к

плоскости П 3


?
= 0

 = (h 1  П 2) обозначить


Рис. 12. Горизонталь
= (h 1  П 3) на чертеже

f   П 2 ; у = const

f 1  0x признак

f 3  0z фронтали

f 2 = f  – свойство фронтали

?
= 0

 = (f 2  П 1) обозначить

 = (f 2  П 3) на чертеже

Рис. 13. Фронталь

р   П 3 ; х = const

р 1  0у признак

р 2  0z профильной прямой

р 3 = р  – свойство профильной

прямой
 = 0


?
= (р 3  П 1) обозначить

 = (р 3  П 2) на чертеже

Рис. 14. Профильная прямая

а  П 1

а 2  0х признак

а 3  0у

?
=

b  П 2

b 1  0х признак

b 3  0z

?
=

c  П 3

c 1  0у признак

с 2  0z

?
=

3 ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПРЯМОЙ
Теорема: Если в пространстве точка принадлежит прямой, то на эпюре проекции этой точки находятся на одноименных проекциях прямой (рис. 18):

М  АВ ,

Е  АВ .
Справедлива обратная теорема :

М 1  A 1 B 1 ;

М 2  A 2 B 2  М  АВ .

4 СЛЕДЫ ПРЯМОЙ
С
?
лед – это точка пересеченная прямой с плоскостью проекций (рис. 19). Так как след принадлежит одной из плоскостей проекций, то его одна координата должна быть равна нулю.

обозначить на H = k ∩ П 1 – горизонтальный след

чертеже (рис. 19) F = k ∩ П 2 – фронтальный след

?
Р = k ∩ П 3 – профильный след

Правило построения следов:

Для построения горизонтального следа прямой ….. необходимо фронтальную проекцию ….. прямой ….. продолжить до пересечения с осью Х , затем из точки пересечения с осью Х восстановить к ней перпендикуляр, и продолжить горизонтальную ….. проекцию прямой …… до пересечения с этим перпендикуляром.

Фронтальный след строиться аналогично.

5 ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ В ДАННОМ СООТНОШЕНИИ
Из свойств параллельного проецирования известно , что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении.

Поэтому, чтобы некоторый отрезок разделить на эпюре в данном соотношении, надо в том же отношении разделить его проекции.

Зная это условие можно определить принадлежность точки К прямой АВ : А 2 К 2 : К 2 В 2 ¹ А 1 К 1 : К 1 В 1 Þ К Ï АВ

Пример: Чтобы разделить отрезок АВ в отношении 2: 3 из точки А 1 проведем произвольный отрезок А 1 В 0 1 разделенный на пять равных частей (рис. 20): A 1 K 0 1 = 2 частям, K 0 1 B 0 1 = 3 частям, А 1 К 0 1 : К 0 1 В 0 1 =2: 3

Соединить точку В 0 1 с точкой В 1 и проведя из точки К 0 1 прямую параллельную (В 1 В 0 1) получим проекцию точки К 1 . Согласно теореме Фалеса (Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону, то на другой стороне отложатся равные между собой отрезки) А 1 К 1: К 1 В 1 = = 2: 3, далее находим К 2 . Таким образом проекции точки К делят одноименные проекции отрезка АВ в данном отношении следовательно и точка К делит отрезок АВ в отношении 2: 3.

6 ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ И УГЛОВ

НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ
Длину отрезка АВ можно определить из прямоугольного треугольника АВС ,гдеA С  = A 1 B 1 , СB  = DZ , угол a - угол наклона отрезка к плоскости П 1 . Для этого на эпюре (рис. 21) из точки B 1 под углом 90  проводим отрезок B 1 B 1 0 = DZ , полученный в результате построений отрезок A 1 B 1 0 и будет натуральной величиной отрезка АВ , а угол B 1 A 1 B 1 0 = α . Рассмотренный метод называется методом прямоугольного треугольника . Однако все построения можно объяснить, как вращение треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П 1 , в этом случае треугольник проецируется на плоскость проекций без искажения. Для определения b - угла наклона отрезка к плоскости П 2 построения аналогичные (рис. 22). Только в треугольнике АВС сторона ВС  = D U и треугольник совмещается с плоскостью П 2 .

? Обозначить проекции прямой и

определить угол α.

Обозначить проекции прямой и

определить угол α.

Обозначить проекции прямой и

определить угол β.

7 ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Прямые в пространстве могут пересекаться, скрещиваться и быть параллельными.

1. Пересекающиеся прямые – это прямые, которые лежат в одной плоскости и имеют общую точку (a ∩ b = K ).

Теорема: Если в пространстве прямые пересекаются , то на чертеже пересекаются их одноименные проекции (рис. 23).

Точка пересечения одноименных проекций находится на одном перпендикуляре к оси Х (К 1 К 2  Ох ).

К = a ∩ b  К  a ; К  b  К 1 = a 1 ∩ b 1 ;

К 2 = a 2 ∩ b 2 .
Справедлива и обратная теорема:

Если К 1  а 1 ; К 2  b 2 , то

К 1 = а 1 ∩ b 1 ;

К 2 = а 2 ∩ b 2  К = а ∩ b .
2. Скрещивающиеся прямые – это прямые, которые не лежат в одной плоскости и не имеют общей точки (рис. 24).

Пары точек 1 и 2 , лежащие на горизонтально-проецирующей прямой называются горизонтально-конкурирующими, а точки 3 и 4 – фронтально-конкурирующими. По ним определяется видимость на эпюре.

По горизонтально-конкурирующим точкам 1 и 2 определяется видимость относительно П 1 . Точка 1 ближе к глазу наблюдателя, она будет видима на плоскости П 1 . Так как точка 1 m , то прямая m будет выше прямой n .

Какая прямая будет видимой по отношению к плоскости П 2 ?
3. Параллельные прямые – это прямые, которые лежат в одной плоскости и имеют несобственную общую точку.

Теорема:

Если в пространстве прямые параллельны, то на чертеже параллельны их одноименные проекции (рис. 25).

Если k  m  k 1  m 1 , k 2  m 2 , k 3  m 3
Справедлива обратная теорема:

Если k 1  m 1 ; k 2  m 2  k  m
Лекция № 3
ПЛОСКОСТЬ

1. Способы задания плоскости на чертеже. Следы плоскости. 2. Положение плоскости относительно плоскостей проекций. 3. Принадлежность точки и прямой плоскости. 4. Главные (особые) линии плоскости.
1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ.

СЛЕД ПЛОСКОСТИ

Плоскость – бесконечная во все стороны линейчатая поверхность, которая на всем своем протяжении не имеет кривизны и преломления.

Плоскость на чертеже может быть задана:

Тремя точками, не лежащими на одной прямой – Р (A , B , C ) , рис. 26.
Прямой и точкой, не лежащей на этой прямой –Р (m , A ; A m ) , рис. 27.
Рис. 29 Рис. 30
Задание плоскости следами
След плоскости – линия пересечения плоскости с плоскостью проекций (рис. 31).
Горизонтальный след получается при пересечении плоскости Р с горизонтальной плоскостью проекций (Р П1 = Р ∩ П 1).
Р П2 = Р ∩ П 2 – фронтальный след ;
Р П3 = Р ∩ П 3 – профильный след ;
Р x , Р y , Р z – точки схода следов .

Положение плоскости в пространстве определяется:

тремя точками, не лежащими на одной прямой;
прямой и точкой, взятой вне прямой;
двумя пересекающимися прямыми;
двумя параллельными прямыми;
плоской фигурой.

В соответствии с этим на эпюре плоскость может быть задана:

проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
проекциями точки и прямой (Рисунок 3.1,б);
проекциями двух пересекающихся прямых (Рисунок 3.1,в);
проекциями двух параллельных прямых (Рисунок 3.1,г);
плоской фигурой (Рисунок 3.1,д);
следами плоскости;
линией наибольшего ската плоскости.

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ 1 , фронтальный – απ 2 и профильный – απ 3 , которые она образует при пересечении с известными плоскостями проекций: горизонтальной π 1 , фронтальной π 2 и профильной π 3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А , В , С ; линии АС , АВ , ВС ; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций .

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями .

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5).

Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

α = m // n

D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости

Упражнение

Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С .


а	б

Рисунок 3.7 – Решение задачи

Решение :

ABCD – плоский четырехугольник, задающий плоскость.
Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
Согласно признаку пересекающихся прямых, построим горизонтальную проекцию точки пересечения этих прямых — K по её известной фронтальной проекции: A 2 C 2 ∩ B 2 D 2 =K 2 .
Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD : на проекции диагонали B 1 D 1 строим К 1 .
Через А 1 К 1 проводим проекцию диагонали А 1 С 1 .
Точку С 1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А 1 К 1 .

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π 1) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π 2) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π 3) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN .

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π 1 . (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение :

Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ 1 (горизонтальный след плоскости);
Точка К должна принадлежать прямой АВ ⇒ К 1 ∈А 1 В 1 и заданной плоскости σ ⇒ К 1 ∈σ 1 , следовательно, К 1 находится в точке пересечения проекций А 1 В 1 и σ 1 ;
Фронтальную проекцию точки К находим посредством линии проекционной связи: К 2 ∈А 2 В 2 .

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.


а	б

Рисунок 3.15 – Пересечение прямой с плоскостью

Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
Если α⊥π 1 , то на плоскость проекций π 1 плоскость α проецируется в прямую (горизонтальный след плоскости απ 1 или α 1), совпадающую с E 1 F 1 ;
Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено );
Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K .

Алгоритм решения задачи (Рисунок 3.15, б):

Через EF проведем вспомогательную плоскость α:

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π 1 или π 2 .

Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций .

Необходимо отдельно определить видимость на каждой плоскости проекций.

Видимость на π 2 (рис. 3.15)

Выберем точки, конкурирующие на π 2 – точки 3 и 4. Пусть точка 3∈ВС∈σ , точка 4∈EF .

Чтобы определить видимость точек на плоскости проекций π 2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π 2 .

Направление взгляда на π 2 показано стрелкой.

По горизонтальным проекциям точек 3 и 4, при взгляде на π 2 , видно, что точка 4 1 располагается ближе к наблюдателю, чем 3 1 .

4 1 ∈E 1 F 1 ⇒ 4∈EF ⇒ на π 2 будет видима точка 4, лежащая на прямой EF , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K

Видимость на π 1

Для определения видимости выберем точки, конкурирующие на π 1 – точки 2 и 5.

Чтобы определить видимость точек на плоскости проекций π 1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π 1 .

Направление взгляда на π 1 показано стрелкой.

По фронтальным проекциям точек 2 и 5, при взгляде на π 1 , видно, что точка 2 2 располагается ближе к наблюдателю, чем 5 2 .

2 1 ∈А 2 В 2 ⇒ 2∈АВ ⇒ на π 1 будет видима точка 2, лежащая на прямой АВ , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.

Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.


а	б

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K .

Построим горизонталь и фронталь в плоскости σ=ΔАВС : A-1 ∈σ; A-1 //π 1 ; С-2 ∈σ; С-2 //π 2 .
Восстановим из точки K перпендикуляр к заданной плоскости: p 1 ⊥h 1 и p 2 ⊥f 2 , или p 1 ⊥απ 1 и p 2 ⊥απ 2

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F ∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

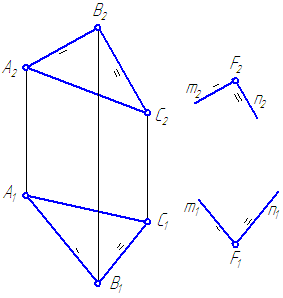
Рисунок 3.17 – Построение плоскости, параллельной заданной

Решение :

В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.

Через точку F проводим прямую m , параллельную, например, АВ .
Через точку F , или же через любую точку, принадлежащую m , проводим прямую n , параллельную, например, ВС , причём m∩ n=F .
β = m ∩n и β//α по определению.

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Порядок построения линии пересечения плоскостей :

Найти точку пересечения горизонтальных следов — это точка М (её проекции М 1 и М 2 , при этом М 1 =М , т.к. М – точка частного положения, принадлежащая плоскости π 1).
Найти точку пересечения фронтальных следов — это точка N (её проекции N 1 и N 2 , при этом N 2 = N , т.к. N – точка частного положения, принадлежащая плоскости π 2).
Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М 1 N 1 и М 2 N 2 .

М N – линия пересечения плоскостей.

Упражнение

Задана плоскость σ = ΔАВС , плоскость α – горизонтально- проецирующая (α⊥π 1) ⇒α 1 – горизонтальный след плоскости (Рисунок 3.19).

Построить линию пересечения этих плоскостей.

Решение :

Так как плоскость α пересекает стороны АВ и АС треугольника АВС , то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.

Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L , то есть K 1 и L 1 , на пересечении горизонтального следа (α 1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС : А 1 В 1 и A 1 C 1 . После чего посредством линий проекционной связи находим фронтальные проекции этих точек K 2 и L 2 на фронтальных проекциях прямых АВ и АС . Соединим одноимённые проекции: K 1 и L 1 ; K 2 и L 2 . Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи :

KL – линия пересечения ΔАВС и σ (α∩σ = KL ).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Заданы плоскости α = m//n и плоскость β = ΔАВС (Рисунок 3.20).

Построить линию пересечения заданных плоскостей.

Решение :

Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π 2 ; τ⊥π 2 .
Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:

— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7);

— результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).

Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях α и β, то есть на прямой пересечения этих плоскостей;
Аналогично находим точку N , общую для плоскостей α и β.
Соединив точки M и N , построим прямую пересечения плоскостей α и β.

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

Упражнение

Заданы плоскости α = ΔАВС и β = a //b . Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение :

Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π 2 , заключив прямую a во вспомогательную плоскость σ (σ∈a ). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а . Следовательно (1-2)∩а =K .

Точка К принадлежит обеим плоскостям α и β.

Следовательно, точка K , является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β.

Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π 2 (τ∈b ).

Соединив точки K и L , получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π 2 и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Решение .

Проведём перпендикуляр CD к плоскости σ – C 2 D 2 ⊥σ 2 (на основании ).

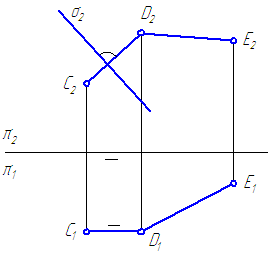
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C 1 D 1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩ DE задают плоскость τ. Итак, τ⊥σ.

Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Задана плоскость α = ΔАВС и точка K вне плоскости α.

Требуется построить плоскость β⊥α, проходящую через точку K .

Алгоритм решения (Рисунок 3.23):

Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС ;
Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости : если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b 2 ⊥f 2 ; b 1 ⊥h 1 ;
Задаём плоскость β любым способом, например, β = a∩ b , таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m //n (Рисунок 3.24). Известно, что K ∈α.

Постройте фронтальную проекцию точки К .

Рисунок 3.24

2. Постройте следы прямой, заданной отрезком CB , и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π 2 , если его диагональ MN //π 2 (Рисунок 3.26).

Рисунок 3.26

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m , исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27

5. Задана плоскость α=a //b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

Рисунок 3.28

6. Задана плоскость α=∆АВС и точка D D плоскость β⊥α и β⊥π 1 .

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE //α и DE //π 1 .